LIMITES INDETERMINADOS

En muchas ocasiones se presenta el cálculo de límites de cocientes, diferencias y productos de funciones en los que al reemplazar la variable por el valor al cual tiende se generan indeterminaciones del tipo . El resultado de estos límites no puede anticiparse y el mismo puede ser cero, ¥ , -¥ , un número finito diferente de cero, o bien puede no existir. Para resolverlos, se realizan procedimientos algebraicos adecuados que permitan salvar la indeterminación.

La indeterminación 0/0

Para salvar indeterminaciones de este tipo, es posible reducir el cociente planteado a otro cuyo denominador no sea cero factorizando el numerador y/o el denominador, cancelando luego los factores comunes. En otras ocasiones, es posible crear un factor común multiplicando el numerador y el denominador por la expresión conjugada de la que se presenta en uno de ellos.

Ejemplo. Halle 

Al sustituir, resulta  y  lo que genera una indeterminación del tipo .

Sin embargo, como  si x ¹ 3, resulta que la función  coincide con la función (x + 3) salvo en x = 3.

Como interesa analizar el comportamiento de la función para valores de x próximos a 3 (por izquierda y por derecha), es posible determinar el comportamiento de  analizando el de la función (x + 3).

Por lo tanto puede decirse que 

Ejemplo. Calcule el valor de .

Al sustituir la variable por 1, tanto el numerador como el denominador se anulan y se genera la indeterminación . Se factorizan el numerador y el denominador y, para x ¹ 1, se simplifican los factores comunes:

La indeterminación ∞-∞

Los procedimientos algebraicos para salvar una indeterminación de este tipo, se desarrollan en los siguientes ejemplos:

   

Ejemplo. Determine el valor de .

Al reemplazar la variable por 2 resulta ¥ -¥ , que es una indeterminación.

Resolviendo la diferencia se obtiene:

Cuando x se aproxima a 2 por derecha, el numerador tiende a –3 y el denominador a 0 por valores mayores que él. Por lo tanto, la expresión resulta negativa y el límite es -¥.

 = -¥

   

Ejemplo. Calcule 

No es posible escribir= ¥ - ¥ , ya que esa diferencia es indeterminada.

Se expresa la función polinomial de la siguiente manera:     = –¥      ya que      x ® +¥     y (2 – x³)® –¥

La indeterminación Ꝏ/Ꝏ

Se analizará el límite del cociente de dos funciones polinomiales en el que la variable crece o decrece indefinidamente. Se debe tener en cuenta que el límite de una función polinomial de grado n ³ 1 cuando x tiende a +¥ ó a -¥ es +¥ ó -¥ . Para resolver límites de este tipo, se dividen el numerador y el denominador de la función dada por xⁿ, siendo n el mayor de los grados de las funciones polinomiales. Luego se aplican las propiedades de los límites.

Ejemplo. Halle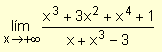 

La función dada consiste en el cociente de dos funciones polinomiales: una de grado 4 y otra de grado 3. Por lo tanto, se dividen el numerador y el denominador por x⁴ y resulta:

 

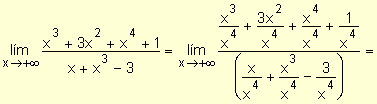
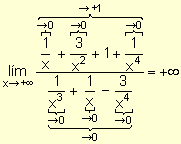
En el ejemplo dado, el grado de la función polinomial del numerador es mayor que el de la del denominador y se obtuvo en este caso ¥.

Ejemplo. Determine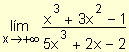 

Se dividen el numerador y denominador por x³:

.

Puede observarse que el ejemplo se refiere al cálculo del límite del cociente de dos funciones polinomiales del mismo grado y se obtuvo como resultado el cociente de los coeficientes de los términos de mayor grado de ambas.

Ejemplo. Calcule .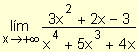

Se dividen el numerador y denominador por x⁴:

En este ejemplo, el grado de la función polinomiales del numerador es menor que el de la del denominador y se obtuvo como resultado cero.

Problema. Un tanque contiene 5000 litros de agua pura. Se bombea al tanque salmuera que contiene 30  gramos  de sal  por  litro  de  agua, a  razón de 25 . La  concentración  de  sal  después  de  t minutos  es: C(t) =  (en ).

a) ¿Cuánto tiempo tiene que transcurrir para que la concentración sea de 10 ?

b) ¿Qué sucede con la concentración cuando el tiempo transcurre indefinidamente?

Solución

a) Para determinar el tiempo que debe transcurrir para que la concentración sea de 10 , se debe igualar la concentración a 10.

10 =  Þ 2000 + 10t = 30t Þ 20t = 2000 Þ t = 100

Es decir, a los 100 minutos la concentración será de 10.

b) Para analizar el comportamiento de la concentración cuando el tiempo transcurre indefinidamente, se debe encontrar el límite cuando t ® +¥ , es decir . Como es un cociente de dos funciones polinomiales, se dividen el numerador y el denominador por t y se obtiene:

Cuando t ® +¥ la concentración tiende a 30 .

La indeterminación 0.∞

Para salvar una indeterminación de este tipo, se pueden realizar distintos procedimientos algebraicos. Algunos de ellos se desarrollan en los siguientes ejemplos.

Ejemplo: Halle 

Cuando x ® –3, x² + 6x +9 ® 0 y , por lo tanto , indeterminado.

Sin embargo,  si x ¹ - 3.

Por lo tanto: 

  

Ejemplo. Calcule 

Como  y , resulta , indeterminado.

En este caso  = , si x ¹ 0.

  

Ejemplo. Halle 

, indeterminado, ya que y .

Sin embargo,  si x ¹ 2.

Por lo tanto: 

REPASO DE LA CLASE 

En el estudio de las funciones hay puntos donde éstas tienen un comportamiento distinto o abstracto, pero en el límite de estos puntos nos encontramos con cosas que no sabemos interpretar y les llamamos indeterminaciones. Veamos cuáles son las que podemos encontrar en el límite de una función:

1. 0 / 0 = indeterminado, no sabemos cuál resultado obtendríamos si se realizara esta operación.
2. (± ∞) / (± ∞) = indeterminado, como no conocemos el valor de éstos números tan grandes no podremos saber con exactitud el resultado.
3. 0 × ∞ = indeterminado, no sabemos si cero por un número en el infinito sea algún valor exacto.
4. ∞ – ∞=indeterminado, no tenemos certeza del resultado de estos números infinitos.

VIDEO: